The simplifying language: Topology
Constructions involving numerous quantifiers are different to grasp. A good theory splits such constructions introducing appropriate notions and building a suitable language. Let 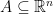 be a subset in the Euclidean space and
be a subset in the Euclidean space and  a metric on it which we (only for simplicity!) will assume translation invariant and denote
a metric on it which we (only for simplicity!) will assume translation invariant and denote  . Everywhere below
. Everywhere below 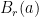 will denote the open ball of radius
will denote the open ball of radius 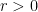 centered at a point
centered at a point 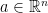 :
: 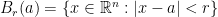 .
.
Definitions. A point 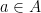 is called interior point, if
is called interior point, if 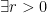 such that the open ball
such that the open ball 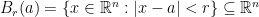 lies in
lies in  , i.e.,
, i.e., 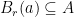 . This is the same as saying that
. This is the same as saying that 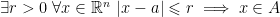 .
.
A point 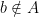 is called exterior point, if it is interior for the complement
is called exterior point, if it is interior for the complement 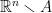 . The points that are neither interior nor exterior are called the boundary points of
. The points that are neither interior nor exterior are called the boundary points of  .
.
The sets of all interior and boundary points of  are denoted
are denoted  and
and 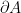 respectively.
respectively.
A point 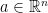 is called an accumulation point (for
is called an accumulation point (for  ), if
), if 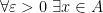 such that
such that 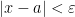 . The set of all accumulation points for
. The set of all accumulation points for  is called its closure and denoted by
is called its closure and denoted by 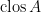 . Sometimes the notation
. Sometimes the notation 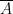 is used for the closure.
is used for the closure.
Exercise. Prove that 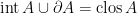 . Prove that the exterior of
. Prove that the exterior of  is
is 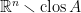 .
.
Exercise. Prove that the notions of interior, exterior and boundary do not depend on the choice of the distance function in 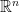 .
.
Definitions. A subset 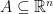 is called open, if it coincides with its own interior,
is called open, if it coincides with its own interior, 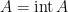 . The subset is closed, if it coincides with its own closure
. The subset is closed, if it coincides with its own closure 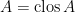 .
.
Exercise. Assume that 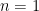 and
and  . Describe interior, closure and boundary of this segment. Is it open? closed? neither?
. Describe interior, closure and boundary of this segment. Is it open? closed? neither?
Exercise. Show that the complement of an open subset is closed and vice versa, the complement of a closed subset is open. Show that Are there other subsets that are both open and closed?
Theorem 1.
 and
and 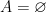 are both open and closed simultaneously.
are both open and closed simultaneously. - Union of any family (infinite or even uncountable) of open sets is open.
- Finite intersection of open sets is open.
- Intersection of any Union of any family (infinite or even uncountable) of closed sets is closed.
- Finite union of closed sets is closed.
Continuity as a topological notion
Consider first the case of maps (functions) defined on the entire Euclidean space, 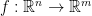 .
.
Temporary Defininion. A map as above will be called an O-map1, if the preimage of any open set 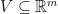 is an open subset
is an open subset 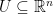 .
.
Lemma 1. A map  continuous at all points of
continuous at all points of 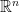 , is an O-map.
, is an O-map.
Proof. Consider any open set  and its preimage
and its preimage 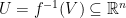 . Let
. Let 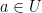 be any point in this preimage: by definition, this means that
be any point in this preimage: by definition, this means that  . Since
. Since  is open in
is open in  , there exists a ball
, there exists a ball 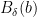 of positive radius
of positive radius  which lies in
which lies in  . By continuity of
. By continuity of  at
at  , there exists
, there exists 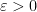 such that
such that 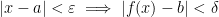 , that is, all points of the ball
, that is, all points of the ball 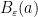 are mapped inside
are mapped inside 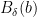 , hence inside
, hence inside  . Therefore the preimage
. Therefore the preimage 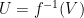 together with the point
together with the point  contains a small ball around
contains a small ball around  , that is,
, that is,  is an interior point for
is an interior point for  . Since
. Since  was chosen arbitrarily, this means that all points of
was chosen arbitrarily, this means that all points of  are interior points, hence
are interior points, hence  is open. Since
is open. Since  was chosen arbitrary, we have proved that
was chosen arbitrary, we have proved that  is an O-map. Q.E.D.
is an O-map. Q.E.D.
Lemma 2. An O-map is continuous at every point 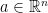 .
.
Proof. Let 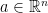 be an arbitrary point, and denote
be an arbitrary point, and denote 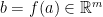 . Consider an arbitrary open ball
. Consider an arbitrary open ball 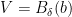 of positive radius
of positive radius  . To prove the continuity of
. To prove the continuity of  , we need to find an open ball around
, we need to find an open ball around 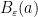 such that its
such that its  -image is inside
-image is inside  . But since
. But since  is open2, its preimage
is open2, its preimage 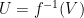 is also open in
is also open in 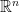 by the definition of an O-map applied to
by the definition of an O-map applied to  . The openness of
. The openness of  means that each its point, in particular, the point
means that each its point, in particular, the point  , is interior for
, is interior for  and hence the ball
and hence the ball 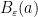 with the required property exists. Q.E.D.
with the required property exists. Q.E.D.
These two lemmas together prove that at least for maps whose domain is the entire Euclidean space, the property “Preimages of open sets are open” (as stated in the Temporary Definition) is fully equivalent to the property of being continuous on the entire domain.
How this result should be modified for maps 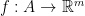 whose domains are only proper subsets of the Euclidean subspace,
whose domains are only proper subsets of the Euclidean subspace, 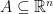 ? The answer is simpler than you might imagine. You don’t need to modify the definition of O-maps, you need to twist the definition of open sets, making it relative to the arbitrary domain
? The answer is simpler than you might imagine. You don’t need to modify the definition of O-maps, you need to twist the definition of open sets, making it relative to the arbitrary domain  of definition of the map
of definition of the map  .
.
Definition. Let 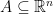 be an arbitrary (not necessarily open) subset of the Euclidean space. A subset
be an arbitrary (not necessarily open) subset of the Euclidean space. A subset 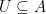 is called open relative to
is called open relative to  , if there exists an open (in the original sense) subset
, if there exists an open (in the original sense) subset 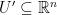 such that
such that 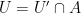 .
.
One can immediately and easily check (by just passing from open sets to relatively open obtained by intersection with any subset  , that:
, that:
- Theorem 1 above remains valid in the relative sense, with the only required correction that the “absolute”
 should replace
should replace 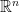 as a set which is both relatively open and relatively closed.
as a set which is both relatively open and relatively closed.
- The proofs of both Lemmas 1 and 2 remain literally true if we replace the (ordinary, absolute) openness by the openness relative to
 : indeed, for
: indeed, for 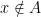 the value
the value 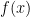 is simply undefined hence cannot violate any inequality or inclusion.
is simply undefined hence cannot violate any inequality or inclusion.
As a result, we obtain the following reformulation of continuity for maps defined on proper subsets of the Euclidean space.
Theorem 2. A map 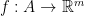 defined on a subset
defined on a subset 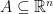 is continuous on its domain of definition, if and only if the preimage
is continuous on its domain of definition, if and only if the preimage 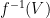 of any open subset
of any open subset 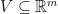 is an open subset relative to
is an open subset relative to  .
.
Note that this equivalent definition of continuity of a map at all points of its domain formally requires only one quantifier, assuming that the notion of an open set is sufficiently familiar to the reader: indeed, it asserts that 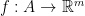 is continuous if and only if
is continuous if and only if
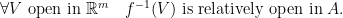
But there is much more to gain from the topological approach.
Topological spaces
The topological language that we introduces in a very particular settings (for subsets of the Euclidean sets) actually works in a much broader context. Indeed, Theorem 1 above is a pretty good motivation for the following definition.
Definition. A topological space  is an abstract set (eventually very large, much larger than subsets of
is an abstract set (eventually very large, much larger than subsets of 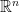 such that some of its subsets are distinguished by bearing a noble name of open sets
such that some of its subsets are distinguished by bearing a noble name of open sets 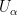 . There are only three axioms these open sets must obey:
. There are only three axioms these open sets must obey:
- The total space
 itself and the empty set
itself and the empty set 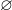 are open.
are open.
- Union of any number of open sets is again open.
- Intersection of any finite number of open sets is open.
Note that the axioms do not specify any way concrete way how open sets should be defined in any concrete example. Only their algebraic properties in the Boolean algebra are important. This is dangerous (examples may challenge our intuition) but provides great versatility. In particular, Theorem 2 above allows to define the continuity for any map 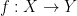 between any two topological spaces, with an immediate trivial corollary that composition of any two continuous maps (when defined) will again be continuous. This becomes a trivial observation (why?), although the proof in the “classical” case is also very easy.
between any two topological spaces, with an immediate trivial corollary that composition of any two continuous maps (when defined) will again be continuous. This becomes a trivial observation (why?), although the proof in the “classical” case is also very easy.
What we (on our rather down-to-earth) level can gain from so abstract constructions? Quite a lot, even if we consider only topological spaces embedded in 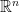 with the supply of open spaces through the definition of relative openness.
with the supply of open spaces through the definition of relative openness.
Connected spaces
Using only topological terms, we can formulate one of the most basic properties of sets, the fact that they do not fall apart as unions of smaller sets. It is instrumental in the study: if something is built from smaller components that do not interact with each other, then one can study these components separately and then “mechanically” bring the results together.
Definition. A topological space  is called disconnected (or disconnect), if it can be represented as a disjoint union of two open sets,
is called disconnected (or disconnect), if it can be represented as a disjoint union of two open sets, 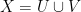 with
with 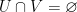 . If such representation is impossible, we call the space connected. Examples are numerous: the Euclidean spaces of all (finite) dimensions are connected, yet the set
. If such representation is impossible, we call the space connected. Examples are numerous: the Euclidean spaces of all (finite) dimensions are connected, yet the set 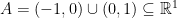 is disconnected, as the two relatively open subsets provide the partition.
is disconnected, as the two relatively open subsets provide the partition.
Remark. The property of connectedness is very closely related to the completeness of the real numbers. One can consider the rational numbers 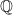 as a topological space and define open and closed sets relative to them. Then the sets
as a topological space and define open and closed sets relative to them. Then the sets 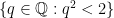 and
and  are obviously (relatively) open and disjoint from each other, but their union is the whole of
are obviously (relatively) open and disjoint from each other, but their union is the whole of 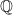 .
.
Theorem 3. A continuous map 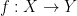 preserves connectedness: if
preserves connectedness: if  is connected, then so is
is connected, then so is  .
.
Proof. Assume that  are two disjoint open subsets such that
are two disjoint open subsets such that  . Then their preimages
. Then their preimages 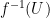 and
and 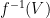 are open by continuity of
are open by continuity of  , obviously disjoint and their union gives
, obviously disjoint and their union gives  in contradiction with the assumption on
in contradiction with the assumption on  . Q.E.D.
. Q.E.D.
Exercise. Describe subsets of  which are connected topological spaces with respect to the relative topology inherited from
which are connected topological spaces with respect to the relative topology inherited from  . Derive from Theorem 4 the familiar Theorem on intermediate value: if a function continuous on a segment
. Derive from Theorem 4 the familiar Theorem on intermediate value: if a function continuous on a segment 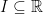 (finite or infinite, doesn’t matter) takes two different values
(finite or infinite, doesn’t matter) takes two different values 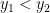 , then it takes also all intermediate values
, then it takes also all intermediate values 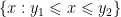 .
.
Warning. One should be very careful and never confuse between preimages and images. The preimage of the connected interval  by the continuous map
by the continuous map 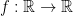 ,
, 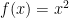 , is the disconnected union
, is the disconnected union 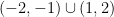 .
.
Another example of a useful notion that is of purely topological nature, is that of an isolated point.
Definition. A point 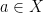 is an isolated point of a topological space
is an isolated point of a topological space  (e.g., a subset
(e.g., a subset 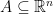 with the topology defined by the relatively open sets), if the one-point subset
with the topology defined by the relatively open sets), if the one-point subset 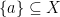 is both open and closed3.
is both open and closed3.
Proposition. Any map 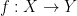 is automatically continuous at all isolated points of
is automatically continuous at all isolated points of  . Q.E.D.
. Q.E.D.
Compact sets
Another purely topological property of topological spaces (in particular, subsets of 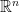 with the inherited relative topology) is a mighty generalization of some finiteness property. Recall that finite collections (say, of positive numbers) allow to choose a minimal element, which will still be positive: infinite collections of positive numbers, like the set
with the inherited relative topology) is a mighty generalization of some finiteness property. Recall that finite collections (say, of positive numbers) allow to choose a minimal element, which will still be positive: infinite collections of positive numbers, like the set 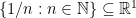 do not allow such choice: the only nonnegative element that is smaller than all number in the above set, is zero which is non-positive.
do not allow such choice: the only nonnegative element that is smaller than all number in the above set, is zero which is non-positive.
Definition. A collection (finite or infinite) of sets  is an open covering of the topological space
is an open covering of the topological space  , if:
, if:
- All sets
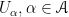 are open, and
are open, and
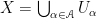 .
.
When dealing with subsets of Euclidean spaces 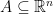 we can assume that a covering
we can assume that a covering 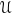 is a collection of open subsets
is a collection of open subsets 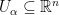 in
in 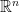 , which contain
, which contain  in their union,
in their union, 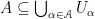 .
.
A subcovering is a subcollection 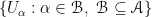 , that is, a collection of open sets which still cover
, that is, a collection of open sets which still cover  obtained by rarefying
obtained by rarefying 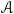 , that is, discarding (throwing away) some open sets from the initial covering.
, that is, discarding (throwing away) some open sets from the initial covering.
Example. Let 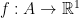 is a function continuous at all points of its domain. Then for every point
is a function continuous at all points of its domain. Then for every point 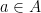 there exists an open set
there exists an open set  such that
such that 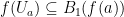 . The collection
. The collection 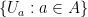 is an open covering of
is an open covering of  . Another example of the covering is the representation of the real line
. Another example of the covering is the representation of the real line  as the union of open sets,
as the union of open sets,
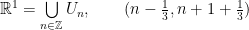 .
.
The second covering is minimal in the sense that removing of any of the sets 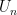 is not covering of
is not covering of  anymore: the middle third of the corresponding segment
anymore: the middle third of the corresponding segment ![[n,n+1]](https://s0.wp.com/latex.php?latex=%5Bn%2Cn%2B1%5D&bg=ffffff&fg=000000&s=0&c=20201002) will become uncovered. Yet some of the coverings are definitely non-minimal, and one can safely remove some of the open sets which were used to cover.
will become uncovered. Yet some of the coverings are definitely non-minimal, and one can safely remove some of the open sets which were used to cover.
Definition. A topological space  (i.e., a set
(i.e., a set 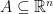 with the inherited topology) is called compact, if any open covering can be decimated to produce a finite open subcovering.
with the inherited topology) is called compact, if any open covering can be decimated to produce a finite open subcovering.
Make no mistake: compactness does not mean that there simply exists finite open covering: any subset can be covered by just one open set (e.g., the space  itself). Compactness means that a finite covering can be achieved by discarding all but finitely many open sets from any open covering. This definition is rather technical, it is somewhat difficult to digest (people rarely have any working intuition with coverings and their finite subcoverings), yet the idea is quite transparent: compact sets possess some hidden “finiteness”. Yet in a very surprising way sometimes compactness can be achieved by adding some points to a non-compact spaces. For instance, the non-compact real interval
itself). Compactness means that a finite covering can be achieved by discarding all but finitely many open sets from any open covering. This definition is rather technical, it is somewhat difficult to digest (people rarely have any working intuition with coverings and their finite subcoverings), yet the idea is quite transparent: compact sets possess some hidden “finiteness”. Yet in a very surprising way sometimes compactness can be achieved by adding some points to a non-compact spaces. For instance, the non-compact real interval 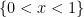 (it is non-compact because the infinite open covering
(it is non-compact because the infinite open covering  cannot be reduced to a finite subcovering) can be compactified by adding two endpoints
cannot be reduced to a finite subcovering) can be compactified by adding two endpoints 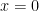 and
and  . The explanation “on one leg” of this phenomenon is simple: adding the extra points imposes additional requirement on the collection of open sets to be a covering, i.e., to cover the extra point as well.
. The explanation “on one leg” of this phenomenon is simple: adding the extra points imposes additional requirement on the collection of open sets to be a covering, i.e., to cover the extra point as well.
Exercise. An unbounded set 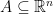 cannot be finite. Indeed, consider the union of all open balls of radius 1 around all points of
cannot be finite. Indeed, consider the union of all open balls of radius 1 around all points of  ,
, 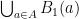 . This is a covering, since each point belongs to “its” ball. Yet no finite subcovering can be selected from this covering: the union of finitely many balls of radius 1 must be bounded. A similar easy argument shows that a set which is not closed, also cannot be compact.
. This is a covering, since each point belongs to “its” ball. Yet no finite subcovering can be selected from this covering: the union of finitely many balls of radius 1 must be bounded. A similar easy argument shows that a set which is not closed, also cannot be compact.
Proposition. The real closed segment ![[0,1]\subseteq\mathbb R^1](https://s0.wp.com/latex.php?latex=%5B0%2C1%5D%5Csubseteq%5Cmathbb+R%5E1&bg=ffffff&fg=000000&s=0&c=20201002) is compact.
is compact.
Proof. Consider an arbitrary open covering  and let
and let ![M\subseteq [0,1]](https://s0.wp.com/latex.php?latex=M%5Csubseteq+%5B0%2C1%5D&bg=ffffff&fg=000000&s=0&c=20201002) be the set of all points
be the set of all points ![a\in[0,1]](https://s0.wp.com/latex.php?latex=a%5Cin%5B0%2C1%5D&bg=ffffff&fg=000000&s=0&c=20201002) such that the subsegment
such that the subsegment ![[0,a]](https://s0.wp.com/latex.php?latex=%5B0%2Ca%5D&bg=ffffff&fg=000000&s=0&c=20201002) admits a finite subcovering selected from
admits a finite subcovering selected from  . Since
. Since 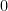 is covered, the set
is covered, the set  contains some positive number. Denote by
contains some positive number. Denote by 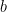 the supremum of points in
the supremum of points in  ,
, 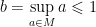 . We claim that
. We claim that  . Indeed, if
. Indeed, if 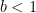 , then
, then 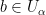 for some open set
for some open set 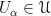 . But since
. But since 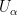 is open, for some sufficiently small
is open, for some sufficiently small 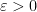 the point
the point 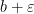 would still be in
would still be in 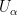 and hence the same finite subcovering will still “serve” the point
and hence the same finite subcovering will still “serve” the point 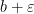 . This contradicts our choice of
. This contradicts our choice of 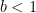 as the exact supremum. This leaves the only possibility that
as the exact supremum. This leaves the only possibility that  , that is, the entire segment
, that is, the entire segment ![[0,1]](https://s0.wp.com/latex.php?latex=%5B0%2C1%5D&bg=ffffff&fg=000000&s=0&c=20201002) admits a finite subcovering selectable from
admits a finite subcovering selectable from 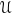 . Q.E.D.
. Q.E.D.
Remark. Compactness of the closed segment ![[0,1]](https://s0.wp.com/latex.php?latex=%5B0%2C1%5D&bg=ffffff&fg=000000&s=0&c=20201002) uses the fact that any bounded set set of real numbers has the exact supremum. Indeed, the “rational closed segment
uses the fact that any bounded set set of real numbers has the exact supremum. Indeed, the “rational closed segment  is not compact. To see this, let us enumerate all points of
is not compact. To see this, let us enumerate all points of 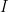 by natural numbers,
by natural numbers,  (this is possible, since
(this is possible, since 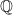 is countable!) and consider the open covering
is countable!) and consider the open covering  which covers each point
which covers each point 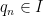 by the interval (open ball) of radius
by the interval (open ball) of radius 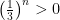 centered at this point. This infinite covering does not admit a finite subcovering of
centered at this point. This infinite covering does not admit a finite subcovering of 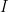 , since the sum of lengths of any finite number of intervals from
, since the sum of lengths of any finite number of intervals from 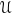 is less than
is less than 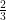 which is less than
which is less than 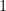 , so at least one point of
, so at least one point of 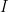 will remain “unserved”.
will remain “unserved”.
Compactness and continuity
Let 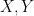 be topological spaces and
be topological spaces and 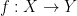 a continuous map.
a continuous map.
Theorem. If  is compact, then its image is
is compact, then its image is 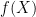 is compact in
is compact in  .
.
Proof. Let  be an arbitrary open covering of
be an arbitrary open covering of  . Consider the sets
. Consider the sets 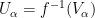 . By continuity of
. By continuity of  , these sets are open and together give a covering $\mathscr U$ of
, these sets are open and together give a covering $\mathscr U$ of  . Since
. Since  is assumed compact, there exists a finite subcovering of
is assumed compact, there exists a finite subcovering of 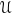 . The corresponding finitely many sets
. The corresponding finitely many sets 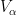 give a finite covering of
give a finite covering of  . Q.E.D.
. Q.E.D.
Combining this Theorem with the Exercise above, we see that any continuous function is bounded on any compact topological space. Note that the preimage of a compact set may well be noncompact (consider any constant function on 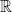 ).
).
Problem. Prove that any closed subset of a compact topological space is also compact.
The following result, which we will not prove, describes all compact subsets of finite-dimensional Euclidean space.
Theorem. A subset 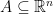 is compact, if and only if it is bounded (i.e.,
is compact, if and only if it is bounded (i.e., 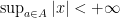 ) and closed (
) and closed (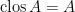 ). Q.E.D.
). Q.E.D.
Warning
The simplicity obtained by carefully crafting the definitions may well be misleading. Open and closed subsets of 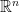 provide a rich basis for our finitely-dimensional intuition. Yet the general notion of a topological space
provide a rich basis for our finitely-dimensional intuition. Yet the general notion of a topological space  without assuming that its topology is inherited from an embedding of
without assuming that its topology is inherited from an embedding of  in some space
in some space 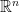 (recall that by “topology” we mean a rule that allows to declare some subsets of
(recall that by “topology” we mean a rule that allows to declare some subsets of  open) allows for some surprising results.
open) allows for some surprising results.
Example. Consider the real line 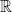 with the origin
with the origin 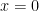 deleted, but with two distinct imaginary points
deleted, but with two distinct imaginary points 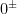 added instead. We can introduce a “perverse topology” on this set
added instead. We can introduce a “perverse topology” on this set 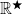 by declaring that the open sets are the open sets in the former
by declaring that the open sets are the open sets in the former 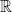 by replacing
by replacing 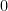 by only one of the two artificially created points
by only one of the two artificially created points 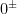 . This rule describes all open subsets of
. This rule describes all open subsets of 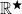 which (check it at home) are consistent with claiming that
which (check it at home) are consistent with claiming that 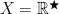 is a topological space.
is a topological space.
What is “wrong” with this space? The answer is very easy: the two distinct points, 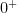 and
and 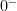 , cannot be separated by disjoint open sets: any two sets
, cannot be separated by disjoint open sets: any two sets  open in the topology of
open in the topology of 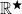 and containing the points
and containing the points 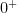 and
and 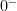 respectively, necessarily intersect:
respectively, necessarily intersect: 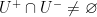 . This means that the topology of
. This means that the topology of 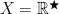 cannot be generated by any distance function on
cannot be generated by any distance function on  . This is an example of the so called non-Hausdorff topology: it happens quite often when dealing with the topological spaces of algebraic origin.
. This is an example of the so called non-Hausdorff topology: it happens quite often when dealing with the topological spaces of algebraic origin.
Example. The same space $\mathbb R^1$ can be equipped with a non-standard topology, the so called Zariski topology: namely, declare closed only finite sets and (and the line itself). Hence open will be complements to finite point sets (and the empty set). This topology is also non-Hausdorff: any two non-empty open sets intersect.
Footnotes